Google Colaboratory Notebook
Run, share, and edit Python notebooks
colab.research.google.com
06-1. 신경망 알고리즘을 벡터화하여 한 번에 전체 샘플을 사용합니다
벡터화된 연산은 알고리즘의 성능을 올립니다
배치 경사 하강법으로 성능을 올립니다
- 확률적 경사하강법: 알고리즘을 1번 반복할 때 1개의 샘플을 사용
- 손실 함수의 전역 최솟값을 불안정하게 찾음
- 선형 회귀, 로지스틱 회귀
- 배치 경사하강법: 가중치를 1번 업데이트 할 때 전체 샘플 사용
- 손실 함수의 전역 최숫값을 안정적으로 찾음
- 알고리즘 1번 수행당 계산 비용 ↑
벡터 연산과 행렬 연산을 알아봅니다
점 곱(dot product, scalar product, 스칼라 곱)
$z=x\cdot w+b$ → $a$: 활성화 함수 → 임계 함수 → $\hat y$
점 곱을 행렬 곱셈으로 표현합니다
$$ XW={\begin{bmatrix}x_1 \space x_2 \space x_3 \end{bmatrix}}{\begin{bmatrix} w_1 \\ w_2 \\w_3\end{bmatrix}}=w_i\times x_i + w_2\times x_3 + w_3 \times x_3 $$
z = np.dot(x, self.w) + self.bnumpy.dot(): 행렬의 곱셈 수행
전체 샘플에 대한 가중치 곱의 합을 행렬 곱셈으로 구합니다
$$ XW={\begin{bmatrix} x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\ & \vdots \\x_{m1} & x_{m2}&x_{m3} \end{bmatrix}}{\begin{bmatrix} w_i\\w_2\\w_3\end{bmatrix}}={\begin{bmatrix} x_{11}w_1+x_{12}w_2+x_{13}w_3 \\ x_{21}w_1+x_{22}w_2+x_{23}w_3 \\ \vdots \\ x_{m1}w_1+x_{m2}w_2+x_{m3}w_3\end{bmatrix}} $$
np.dot(x, w)SingleLayer 클래스에 배치 경사 하강법 적용하기
1. 라이브러리 임포트하기
import numpy as np
import matplotlib.pyplot as plt2. 위스콘신 유방암 데이터 세트를 훈련, 검증, 테스트 세트로 나누고 데이터 살펴보기
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify=y, test_size=0.2, random_state=42)
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)3. 데이터 크기 확인하기
print(x_train.shape, x_val.shape) #(364, 30) (91, 30)4. 정방향 계산을 행렬 곱셈으로 표현하기
$$ XW+b={\begin{bmatrix} x_1^{(1)} & \cdots & x_{30}^{(1)} \\ \vdots & & \vdots \\ x_1^{(364)} & \cdots & x_{30}^{(364)} \end{bmatrix}} {\begin{bmatrix} w_1\\w_2\\\vdots \\ w_{30}\end{bmatrix}} + {\begin{bmatrix} b \\ \vdots \\ b\end{bmatrix}}={\begin{bmatrix} z^{(1)} \\ z^{(2)} \\ \vdots \\ z^{(364)}\end{bmatrix}} $$
$$ {\begin{bmatrix} x_1^{(1)} & \cdots & x_{30}^{(1)} \\ \vdots & & \vdots \\ x_1^{(364)} & \cdots & x_{30}^{(364)} \end{bmatrix}} {\begin{bmatrix} w_1\\w_2\\\vdots \\ w_{30}\end{bmatrix}} + b={\begin{bmatrix} x_1^{(1)}w_1+x_2^{(1)}w_2+\cdots+x_{30}^{(1)}w_{30} \\ \vdots \\ x_1^{(364)}w_1+x_2^{(364)}w_2+\cdots+x_{30}^{(364)}w_{30} \end{bmatrix}}+b={\begin{bmatrix} x_1^{(1)}w_1+x_2^{(1)}w_2+\cdots+x_{30}^{(1)}w_{30}+b \\ \vdots \\ x_1^{(364)}w_1+x_2^{(364)}w_2+\cdots+x_{30}^{(364)}w_{30}+b \end{bmatrix}} $$
5. 그레디언트 계산 이해하기
$$ X^TE={\begin{bmatrix} x_1^{(1)} & \cdots & x_1^{(364)} \\ x_2^{(1)} & \cdots & x_2^{(364)} \\ \vdots & & \vdots \\ x_{30}^{(364)} & \cdots & x_{30}^{(364)}\end{bmatrix}} {\begin{bmatrix} e^{(1)} \\ e^{(2)} \\ \vdots \\ e^{(364)}\end{bmatrix}} = {\begin{bmatrix} g_1 \\ g_2 \\ \vdots \\ g_{30} \end{bmatrix}} $$
- $X$: (364, 30)
- $X^T$: (30, 364). 행렬 곱셈을 위해 $X$를 전치하여 사용
- $E$: (364, 1)
- $G$: (30, 1)
6. forpass(), backprop() 메서드에 배치 경사 하강법 적용하기
def forpass(self, x):
z = np.dot(x, self.w) + self.b #선형 출력
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m #가중치에 대한 평균 그레디언트
b_grad = np.sum(err) / m #절편에 대한 평균 그레디언트
return w_grad, b_grad7. fit() 메서드 수정하기
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.w = np.ones((x.shape[1], 1))
self.b = 0
self.w_history.append(self.w.copy())
for i in range(epochs):
z = self.forpass(x)
a = self.activation(z)
err = -(y - a)
w_grad, b_grad = self.backprop(x, err)
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss())/ m)
self.update_val_loss(x_val, y_val)numpy.reshape(): 배열 차원 재구조화reshape(-1, column): (1, column)의 크기로 재구조화 *행렬에서 벡터는 (-1, 1)로 나타냄reshape(row, -1): (row, 1)의 크기로 재구조화
numpy.ones(shape, dtype, order): 1로 가득찬 array 생성numpy.clip(array, min, max): array 내의 요소들에 대해서 min보다 작은 값들은 min으로, max보다 큰 값은 max로 바꿈
8. 나머지 메서드 수정하기
def predict(self, x):
z = self.forpass(x)
return z > 0
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.activation(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = np.sum(-(y_val*np.log(a) + (1-y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))#SingleL:ayer 클래스 전체 코드
class SingleLayer:
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.w_history = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
def forpass(self, x):
z = np.dot(x, self.w) + self.b
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m
b_grad = np.sum(err) / m
return w_grad, b_grad
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.w = np.ones((x.shape[1], 1))
self.b = 0
self.w_history.append(self.w.copy())
for i in range(epochs):
z = self.forpass(x)
a = self.activation(z)
err = -(y - a)
w_grad, b_grad = self.backprop(x, err)
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss())/ m)
self.update_val_loss(x_val, y_val)
def predict(self, x):
z = self.forpass(x)
return z > 0
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val)
a = self.activation(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss = np.sum(-(y_val*np.log(a) + (1-y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
def activation(self, z):
a = 1 / (1 + np.exp(-z))
return a
def score(self, x, y):
return np.mean(self.predict(x) == y.reshape(-1, 1))
def reg_loss(self):
return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)9. 훈련 데이터 표준화 전처리하기
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_val_scaled = scaler.transform(x_val)- sklearn.preprocessing: 데이터 전처리 관련 클래스(변환기, transformer) 포함
StandardScaler(): 데이터 세트의 특성을 평균이 0, 표준 편차가 1이 되도록 표준화하는 클래스
10. 배치 경사 하강법 적용하기
확률적 경사 하강법은 훈련 세트의 샘플 개수*에포크 만큼 가중치 업데이트가 일어나지만, 배치 경사 하강법의 경우 에포크만큼의 가중치 업데이트가 일어나므로 확률적 경사 하강법보다 훨씬 더 큰 에포크 횟수를 지정해줘야 한다.
single_layer = SingleLayer(l2=0.01)
single_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=10000)
single_layer.score(x_val_scaled, y_val) #0.97802197802197811. 검증 세트로 성능 측정하고 그래프로 비교하기
plt.ylim(0, 0.3)
plt.plot(single_layer.losses)
plt.plot(single_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(['train_loss', 'val_loss'])
plt.show()
손실값이 안정적으로 감소한다.
12. 가중치의 변화 그래프로 나타내기
w2 = []
w3 = []
for w in single_layer.w_history:
w2.append(w[2])
w3.append(w[3])
plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')
plt.xlabel('w[2]')
plt.ylabel('w[3]')
plt.show()
06-2. 2개의 층을 가진 신경망을 구현합니다
하나의 층에 여러 개의 뉴런을 사용합니다

$$ \begin{matrix}x_1w_{11}+x_2w_{21}+x_3w_{31}+b_1=z_1 \\ w_1w_{12}+x_2w_{22}+x_3w_{32}+b_2=z_2 \end{matrix} $$
$$ {\begin{bmatrix} x_1 \space x_2 \space x_3 \end{bmatrix}}{\begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \\ w_{31} & w_{32} \end{bmatrix}}+{\begin{bmatrix}b_1 \space b_2 \end{bmatrix}}={\begin{bmatrix}z_1 \space z_2 \end{bmatrix}} $$
$$ XW_i+b_i=Z_i $$
출력을 하나로 모읍니다

$$ a_1w_1+a_2w_2+b_2=z\space\space (선형\space방정식) $$
$$ {\begin{bmatrix} a_1\space a_2\end{bmatrix}}{\begin{bmatrix} w_i \\w_2\end{bmatrix}}+b_2=z \space\space(행렬\space곱셈) $$
$$ A_1W_2+b_2=Z_2 $$
은닉층이 추가된 신경망을 알아봅니다

입력과 출력은 행렬로 표기합니다

- $X$: 입력 행렬
- $W$: 가중치 행렬
- $b$: 절편
- $Z$: 출력
- $A$: 활성화 출력
- $\hat Y$: 예측값
다층 신경망의 개념을 정리합니다

활성화 함수는 층마다 다를 수 있지만 한 층에서는 같아야 합니다
활성화 함수를 검은색 원으로 선형 함수의 출력값인 $z$ 뉴런의 바로 오른쪽에 붙여 표시하였다. 은닉층은 알고리즘에 따라 하나가 아니라 여러 개로 늘어날 수 있는데, 이때 같은 층의 활성화 함수는 모두 같아야 한다.
완전 연결(fully-connected) 신경망
입력층-은닉층, 은닉층-출력층 사이의 뉴런들이 모두 연결되어 있는 신경망을 완전 연결 신경망이라고 한다.
층과 층 사이의 데이터 흐름이 한쪽 방향으로만 진행된다.
다층 퍼셉트론, 밀집 연결(densely-connected) 신경망, 피드 포워드(feed forward) 신경망이라고도 불린다.
순환 신경망(Recurrent Neural Network, RNN)
데이터 흐름이 순환되는 신경망
자연어 처리에 주로 이용된다.
합성곱 신경망(Convolutional Neural Network, CNN)
데이터가 흐르지만 완전히 연결되어 있지 않은 신경망
이미지 처리 등에 이용된다.
다층 신경망에 경사 하강법을 적용합니다

가중치에 대하여 손실 함수를 미분합니다(출력층)
$$ \frac{\partial L}{\partial W_2}=\frac{\partial L}{\partial Z_2}\frac{\partial Z_2}{\partial W_2} $$
$$ \frac{\partial L}{\partial Z_2}=-(Y-A_2) $$
$$ \frac{\partial Z_2}{\partial W_2}=A_1 $$
도함수를 곱합니다(출력층)
$$ \frac{\partial L}{\partial W_2} =\frac{\partial L}{\partial Z_2}\frac{\partial Z_2}{\partial W_2} =A_1^T(-(Y-A_2)) $$
절편에 대하여 손실 함수를 미분합니다(출력층)
$$ \frac{\partial L}{\partial b_2} =1^T(-(Y-A_2)) $$
가중치에 대하여 손실 함수를 미분합니다(은닉층)
$$ \frac{\partial L}{\partial W_1} =\frac{\partial L}{\partial Z_2} \frac{\partial Z_2}{\partial A_1} \frac{\partial A_1}{\partial Z_1} \frac{\partial Z_1}{\partial W_1} $$
도함수를 곱합니다(은닉층)
$$ \frac{\partial Z_1}{\partial Z_1} =X $$
$$ \frac{\partial A_1}{\partial Z_1} =A_1 ◉(1-A_1) $$
절편에 대하여 손실 함수를 미분하고 도함수를 곱합니다
$$ \frac{\partial L}{\partial W_1} =\frac{\partial L}{\partial Z_2} \frac{\partial Z_2}{\partial A_1} \frac{\partial A_1}{\partial Z_1} \frac{\partial Z_1}{\partial W_1} =1^T(-(Y-A_2)W^T_2◉A_1◉(1-A_1)) $$
2개의 층을 가진 신경망 구현하기
1. SingleLayer 클래스를 상속한 DualLayer 클래스 만들기
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units #은닉층의 뉴런 개수
self.w1 = None
self.b1 = None
self.w2 = None
self.b2 = None
self.a1 = None
self.losses = []
self.val_losses = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l22. forpass() 메서드 수정하기
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1
self.a1 = self.activation(z1)
z2 = np.dot(self.a1, self.w2) + self.b2
return z2numpy.dot(): 행렬 곱 연산ndarray.T: 행렬 전치
3. backprop() 메서드 수정하기
def backprop(self, x, err):
m = len(x)
w2_grad = np.dot(self.a1.T, err) / m
b2_grad = np.sum(err) / m
err_to_hidden = np.dot(err, self.w2.T) * self.a1 * (1 - self.a1)
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad4. fit() 메서드 수정하기
5. init_weights()로 가중치 초기화하기
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units)) #(특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units)
self.w2 = np.ones((self.units, 1))
self.b2 = 06. fit() 메서드의 일부를 training(). 메서드로 분리하기
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
y_val = y_val.reshape(-1, 1)
m = len(x)
self.init_weights(x.shape[1])
for i in range(epochs):
a = self.training(x, y, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
self.update_val_loss(x_val, y_val)
def training(self, x, y, m):
z = self.forpass(x)
a = self.activation(z)
err = -(y - a)
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a7. reg_loss() 메서드 수정하기
def reg_loss(self):
return self.l1 * (np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + self.l2 / 2 * (np.sum(self.w1**2) + np.sum(self.w2**2))모델 훈련하기
1. 다층 신경망 모델 훈련하고 평가하기
dual_layer = DualLayer(l2=0.01)
dual_layer.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=20000)
dual_layer.score(x_val_scaled, y_val) #0.9780219780219782. 훈련 손실과 검증 손실 그래프 분석하기
plt.ylim(0, 0.3)
plt.plot(dual_layer.losses)
plt.plot(dual_layer.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()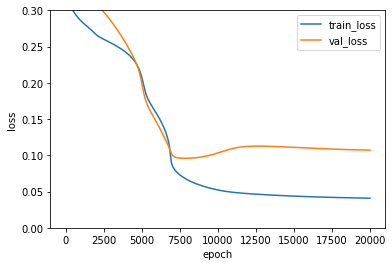
위스콘신 유방암 데이터는 특성이 30개로, SingleLayer는 가중치 30개와 절편 1개를 필요로 했다. DualLayer의 경우 은닉층의 뉴런 개수가 총 10개 이므로 30*10+10개의 가중치와 10+1개의 절편을 학습해야 한다. 즉, SingleLayer보다 훨씬 더 많은 가중치와 절편을 학습해야 하므로 loss 값이 느리게 줄어든다. 따라서 가중치 초기화 방법을 개선해야 한다.
가중치 초기화 개선하기
1. 가중치 초기화를 위한 init_weights() 메서드 수정하기
class RandomInitNetwork(DualLayer):
def init_weights(self, n_features):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_features, self.units))
self.b1 = np.zeros(self.units)
self.w2 = np.random.normal(0, 1, (self.units, 1))
self.b2 = 0numpy.random.normal(mean, std, N): 정규 분포를 따르는 난수 배열 생성
2. 모델 훈련시키기
random_init_net = RandomInitNetwork(l2=0.01)
random_init_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
plt.ylim(0, 0.8)
plt.plot(random_init_net.losses)
plt.plot(random_init_net.val_losses)
plt.legend(['train_loss', 'val_loss'])
plt.show()
앞서 DualLayer에서 초깃값을 1로 설정(np.ones())를 사용했을 때보다 RandomInitNetwork에서 초깃값을 무작위로 초기화했을 때 훨씬 빠르게 손실 함수 값이 감소한다.
06-3. 미니 배치를 사용하여 모델을 훈련합니다
미니 배치 경사 하강법을 알아봅니다
미니 배치 경사 하강법은 전체 데이터를 조금씩 나누어(미니 배치) 가중치를 업데이트하는 방법으로, 데이터 1개에 대해 가중치를 업데이트하는 확률적 경사 하강법과 전체 데이터에 대해 가중치를 업데이트하는 배치 경사하강법의 절충안이라고 할 수 있다. 미니 배치의 크기가 작으면 확률적 경사 하강법처럼 손실 함수가 불안정하게 감소하고, 미니 배치의 크기가 크면 배치 경사 하강법처럼 안정적으로 감소할 것이다.
미니 배치의 크기는 대체로 2의 배수를 사용하는 하이퍼 파라미터(hyperparameter)이다.
미니 배치 경사 하강법을 구현합니다
1. MinibatchNetwork 클래스 구현하기
RandomInitNework 클래스를 상속받고, __init__()에 미니 배치 하이퍼 파라미터(batch_size)를 추가한다.
class MinibatchNetwork(RandomInitNetwork):
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
super().__init__(units, learning_rate, l1, l2)
self.batch_size = batch_size2. fit() 메서드 수정하기
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1)
self.init_weights(x.shape[1])
np.random.seed(42)
for i in range(epochs):
loss = 0
for x_batch, y_batch in self.gen_batch(x, y):
y_batch = y_batch.reshape(-1, 1)
m = len(x_batch)
a = self.training(x_batch, y_batch, m)
a = np.clip(a, 1e-10, 1-1e-10)
loss += np.sum(-(y_batch*np.log(a) + (1-y_batch)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val)3. gen_batch() 메서드 만들기
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size
if length % self.batch_size:
bins += 1
indexes = np.random.permutation(np.arange(len(x)))
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size * i
end = self.batch_size * (i + 1)
yield x[start:end], y[start:end]- 제너레이터(generator): 순차적으로 데이터에 접근할 수 있는 반복 가능한 객체(iterator) 반환. 명시적으로 리스트를 만들지 않으면서 필요한 만큼 데이터를 추출할 수 있어 메모리를 보다 더 효율적으로 사용할 수 있다.
yield: 결괏값을 한 번에 반환하는 return과는 달리, 여러 번에 나누어 결괏값을 반환한다.
4. 미니 배치 경사 하강법 적용하기
minibatch_net = MinibatchNetwork(l2=0.01, batch_size=32)
minibatch_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
minibatch_net.score(x_val_scaled, y_val) #0.978021978021978plt.plot(minibatch_net.losses)
plt.plot(minibatch_net.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
에포크마다 훈련 반복이 여러 번 일어나므로 수렴 속도가 빨라진다.
5. 미니 배치 크기 늘려서 그래프 그리기
minibatch_net = MinibatchNetwork(l2=0.01, batch_size=128)
minibatch_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
minibatch_net.score(x_val_scaled, y_val) #0.978021978021978
plt.plot(minibatch_net.losses)
plt.plot(minibatch_net.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
minibatch_net = MinibatchNetwork(l2=0.01, batch_size=512)
minibatch_net.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val, epochs=500)
minibatch_net.score(x_val_scaled, y_val) 0.978021978021978
plt.plot(minibatch_net.losses)
plt.plot(minibatch_net.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
미니 배치 크기를 늘리면 손실 그래프가 안정적으로 감소하는 대신 수렴 속도가 느려진다. 일반적으로 미니 배치의 크기는 32~512개 사이의 값으로 지정한다.
사이킷런 사용해 다층 신경망 훈련하기
- MLPClassifier: 분류 작업을 위한 클래스
hidden_layer_sizes: 은닉층의 수와 뉴런의 개수를 튜플로 지정. 기본값 (100, )activation: 활성화 함수 지정. 기본값 ReLUsolver: 경사 하강법 알고리즘 종류 지정. 기본값 sgdalpha: L2 규제값 지정. 기본값 0.0001batch_size: 배치 크기. 기본값 200learning_rate_init: 학습률 초깃값max_iter: 에포크 횟수
1. MLPClassifier의 객체 만들기
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(hidden_layer_sizes=(10,), activation='logistic', solver='sgd', alpha=0.01, batch_size=32, learning_rate_init=0.1, max_iter=500)2. 모델 훈련하기
mlp.fit(x_train_scaled, y_train)
mlp.score(x_val_scaled, y_val) #0.989010989010989'인공지능' 카테고리의 다른 글
| 생성형 AI와 LLM(Large-Language Model)에 대하여 (1) | 2025.02.09 |
|---|---|
| 강화학습의 이해 (2) | 2025.01.26 |
| [Do it! 딥러닝 입문 리뷰] 5장. 훈련 노하우를 배웁니다 (1) | 2022.02.19 |
| [Do it! 딥러닝 입문 리뷰] 4장. 분류하는 뉴런을 만듭니다 - 이진분류 (0) | 2022.02.19 |
| [Do it! 딥러닝 입문 리뷰] 3장. 머신러닝의 기초를 다집니다 - 수치예측 (0) | 2022.02.16 |